Slide talk: Demystifying GPT-3

The transformer

For another meeting of our reinforcement/machine learning reading group, I gave a talk on the underlying model of GPT-2 and GPT-3, the ‘Transformer’. There are two main concepts I wanted to explain: positional encoding and attention.

During the talk, I found that two things were most confusing. The first is the definition of positional encoding. Indeed, it's just a deterministic vector added to each word, based on its position. The second is the way attention is visualised as a heatmap with the input sentence on both axes. This I found quite puzzling at first, and in many places it was not really explained properly. Below, I will clarify these two things. For the slides, which can be used as an introduction to this post, see here. Many references to other introductory sources can also be found there.

Positional encoding

Positional encoding makes up for the lack of ‘sequentialness’ of the input data by placing an encoded sequence of words (each word being a vector in \(\mathbb{R}^{d_{\text{model}}}\)) on a kind of spiral staircase in \(\mathbb{R}^{N \times d_\text{model}}\). The \(t\)-th step of the staircase is the vector \[ e(t) = \left( \begin{matrix} \sin(\omega_1 t) \\ \cos(\omega_1 t) \\ \vdots \\ \sin(\omega_{d_{\text{model}} / 2} t) \\ \cos(\omega_{d_{\text{model}} / 2} t) \\ \end{matrix} \right) \] where \(\omega_k = {10000^{- \frac{2k}{d_\text{model}}}}\). These steps are simply added to corresponding word in the input sequence. Since the added values are nicely bounded, they are harmless to add to the embedding layer. But the interesting property they have is that going up the staircase by a fixed number of steps is a linear operation. That is, there is a linear transformation \(T\), such that for every \(k, t\): \[ e(t + k) = T^k e(t) \] A proof can be found here. According to the original paper, this allows the model 'to easily learn to attend by relative positions'.

Attention

The most important ingredient of the transformer are attention layers. For simplicity, I restrict to the self-attention layers in the encoding part of the transformer here. These precede the feed-forward layers in the encoder. They are supposed to equip an input sentence with a representation of ‘context’. In a single attention head, this context is a linearly transformed representation of the input sequence, weighted by attention.

Self-attention is learned by the model in the following way. An input word \(\vec{w} \in \mathbb{R}^{d_\text{model}}\) is transformed by a linear network layer into a key and a corresponding value: \[ \vec{k} = W^K \vec{w} \qquad \vec{v} = W^V \vec{w} \]

On top of this, each word may be transformed into a query, which has the same dimension as a key. \[ \vec{q} = W^Q \vec{w} \] Any query can act on any key by taking the inner product. Given a query \(\vec{q}\), the attention applied to the value \(\vec{v}\) of a key \(\vec{k}\) is given by a softmaxed scaled dot-product: \[ \text{Attention}(\vec{q}, \vec{k}, \vec{v}) = \text{softmax} \left( \frac{\vec{q} \cdot \vec{k}}{\sqrt{d_\text{model}}} \right) \vec{v} \] In the model, the attention to a value is computed as the sum of the attention over all queries generated from the input sequence. So what the attention head does is multiply the values \(V\) with an attention matrix: \[ \text{Attention}({Q}, {K}, {V}) = \text{softmax}\left(\frac{{Q}{K}^T}{\sqrt{d_\text{model}}} \right) {V} \] where the rows of \(Q, K, V\) are all queries, keys and values computed from the input sequence.

This attention matrix can be visualised. Since every pair of words determines a query and a key, it computes some attention. This can be visualised in a heatmap, where the axes are labelled by the input sentence. An example can be found in the The Annotated Transformer by Harvard NLP:

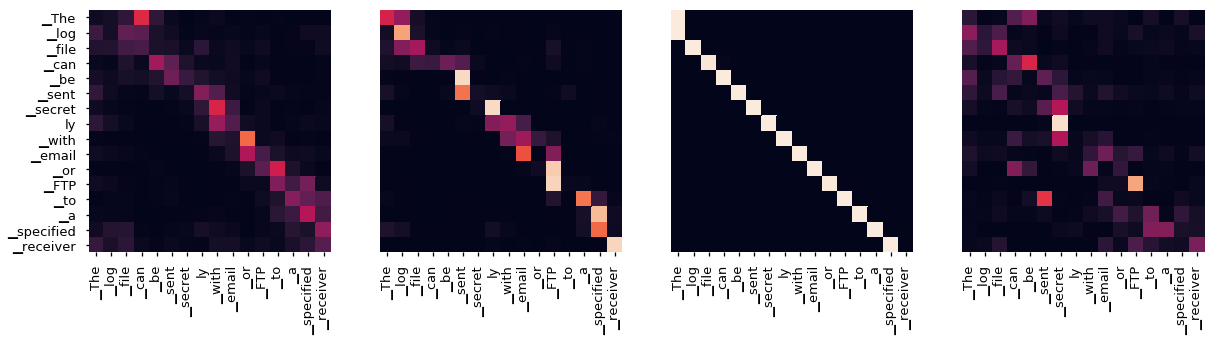
The picture displays the attention weights in the first four self-attention heads in the second encoder layer. But note that the labels on the axes do not really indicate the words themselves. Rather, they are learned linear transformations of words. The vertical axis contains the queries, and the horizontal axis contains the keys. Interestingly, the third head seems to have learned to turn words into queries that, given the input keys, instruct to pay attention to the value corresponding to the word preceding the word corresponding to the query. Learning this type of shifts in position is exactly what positional encoding is supposed to enable!